categorieën: Aanbevolen artikelen » Beginnende elektriciens
Aantal keer bekeken: 57937
Reacties op het artikel: 4
Booleaanse algebra. Deel 3. Contactschema's
 Het artikel beschrijft de basisprincipes van het ontwerpen van relaisschakelingen in overeenstemming met een bepaald algoritme van hun werking.
Het artikel beschrijft de basisprincipes van het ontwerpen van relaisschakelingen in overeenstemming met een bepaald algoritme van hun werking.
In twee vorige artikelen werd verteld over de basis Booleaanse algebra en relay-algebra. Op basis hiervan werden structurele formules ontwikkeld, waarop al typische contactcircuits werden ontwikkeld.
Het opstellen van een structuurformule volgens een kant-en-klaar schema is eenvoudig. Het is veel moeilijker om het elektrische circuit van de toekomstige machine te presenteren volgens de kant-en-klare structuurformule. Het heeft wat training nodig!
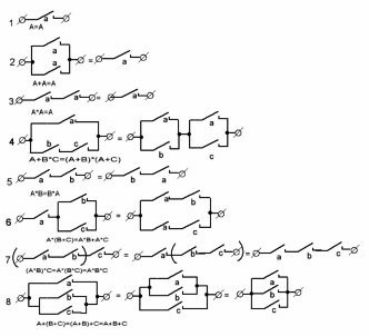
Afbeelding 1 toont de meest voorkomende opties. contact circuits en hun equivalenten. Ze zullen helpen bij het voorbereiden van elektrische circuits van machines, evenals het analyseren van kant-en-klare structuren, bijvoorbeeld bij het repareren ervan.
Hoe kunt u de hierboven besproken opties voor contactcircuits gebruiken?
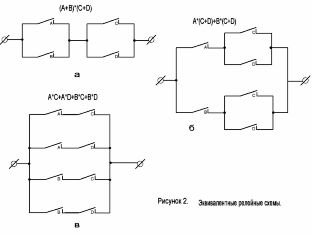
Overweeg het circuit getoond in figuur 2, a. De bijbehorende structuurformule heeft de vorm: (A + B) * (C + D).
Met behulp van de distributiewet van de Booleaanse algebra openen we de haakjes in deze uitdrukking en krijgen: A * (C + D) + B * (C + D), wat overeenkomt met het schema in Afbeelding 2, b. Verder kunnen we door vermenigvuldiging de formule A * C + A * D + B * C + B * D verkrijgen, die overeenkomt met figuur 2, c.
Alle drie de regelingen zijn gelijkwaardig, dat wil zeggen dat ze onder dezelfde voorwaarden worden afgesloten. Ze zijn echter verschillend in complexiteit.
Figuur 1. Typische contactcircuits
De eerste van de circuits, de eenvoudigste, vereist vier relais, die elk een normaal open contact moeten hebben. (Om de tekeningen te vereenvoudigen, worden relaisspoelen niet weergegeven).
Schema "b" vereist een relais met twee contactgroepen. De hoofdtaak van de algebra van contactcircuits is eigenlijk om alle equivalente circuits te vinden, zodat je de eenvoudigste daarvan kunt kiezen.
Figuur 2. Gelijkwaardige contactcircuits.
Probeer de volgende problemen zelf op te lossen om het behandelde materiaal te consolideren.
1. Teken het schakelschema van een automaat met de structuurformule A * B * C * D + A * B * E + A * D.
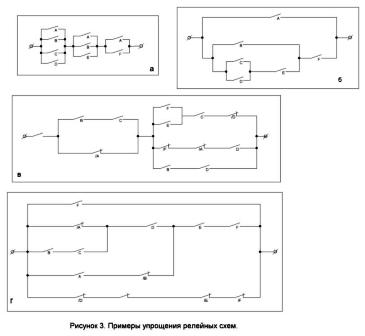
2. Bewijs dat de schakelingen in figuur 3, a en b, equivalent zijn.
3. Vereenvoudig het circuit weergegeven in figuur 3, c.
4. Welke structuurformule implementeert het schema in figuur 3, d?
Na wat we al hebben bestudeerd, zal het mogelijk zijn om te beginnen met het oplossen van de problemen die zich aan het begin van het eerste artikel hadden voorgedaan. We herinneren ons ze kort.
De eerste taak was om de gloeilamp in de kamer aan en uit te zetten met drie schakelaars op verschillende plaatsen: aan de deur, aan de tafel, aan het bed.
De tweede taak is om te stemmen op sportrechters: van de vier juryleden moet “VOOR” minstens twee stemmen, op voorwaarde dat “VOOR” de voorzitter van de commissie heeft gestemd.
De derde taak was alleen voor educatieve doeleinden. Het stelde hetzelfde voor als in de eerste, alleen voor zes schakelaars, alsof er zes muren in de kamer waren. Soortgelijke circuits worden net ontwikkeld met behulp van de algebra van relaiscircuits.
Over het algemeen kunnen we dit probleem op twee verschillende manieren aanpakken als we een schema willen ontwikkelen dat bepaalde logische eigenschappen heeft. Gewoonlijk kunnen deze paden "intuïtief" en "algebraïsch" worden genoemd.
Sommige taken worden op de eerste manier beter opgelost, terwijl andere op de tweede manier. De intuïtieve benadering blijkt handiger wanneer de werking van het circuit wordt geregeld door veel schakelaars, maar er is enige symmetrie in de onderlinge opstelling van deze relais. We zullen zien dat hier een intuïtieve aanpak sneller tot het doel leidt, terwijl het gebruik van het apparaat van relay-algebra in het geval van veel variabelen erg omslachtig kan zijn. Het is nuttig om kennis te maken met beide mogelijke benaderingen om dit probleem op te lossen.
Laten we beginnen met een intuïtieve aanpak. Stel dat we een circuit moesten bouwen dat gesloten was toen alle n stuurrelaiscircuits werkten.
De oplossing voor dit probleem vereist geen lange beraadslaging: het is duidelijk dat aan de ingestelde voorwaarde zal worden voldaan als opeenvolgend verbonden n normaal open relaiscontacten.
Evenzo is het duidelijk dat om een circuit te bouwen dat sluit wanneer ten minste een van de n relais is geactiveerd, het voldoende is om n normaal open relaiscontacten parallel aan te sluiten.
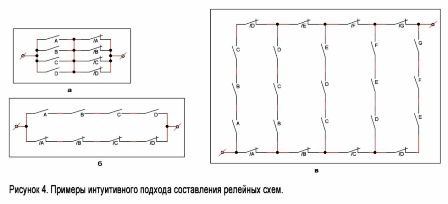
Het is gemakkelijk om een circuit voor te stellen dat sluit wanneer sommige, maar niet alle, relais worden geactiveerd. Een dergelijke schakeling is weergegeven in figuur 4, a. Rechts ziet u een diagram dat werkt volgens het principe "alles of niets". Het zal alleen worden gesloten wanneer alle relais worden uitgeschakeld of de relais worden losgekoppeld (Afbeelding 4, 6).
Beschouw nu een complexer voorbeeld. Stel dat er n contacten zijn in een bepaalde specifieke volgorde: A, B, C, D, E, F ... We construeren een circuit dat sluit wanneer alle in serie verbonden contacten worden gesloten, en alleen zij zijn. Een dergelijk schema voor de waarden n = 7 en k = 3 is weergegeven in figuur 4, c. De methode voor het construeren van dergelijke schema's voor alle andere waarden van n en k is duidelijk uit deze figuur.
We gaan door met het bouwen van circuits volgens de gegeven omstandigheden van hun werk met behulp van relaisalgebra.
Zoals eerder worden de bedrijfsomstandigheden van het circuit altijd altijd eerst mondeling ingesteld. De ontwerper moet allereerst onder woorden kunnen brengen wat hij wil. Als hij niet zo duidelijk is, zal geen algebra helpen. U moet altijd beginnen met een duidelijke verklaring van de vereisten die voor het nieuwe schema worden gesteld. Zoals in elk bedrijf is deze taak misschien het moeilijkst. Als de voorwaarden eenvoudig genoeg zijn, kunnen we onmiddellijk een uitdrukking schrijven van een structuurformule die aan deze vereisten voldoet.
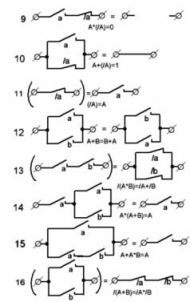
Voorbeeld 1 Stel dat we een circuit moeten bouwen met 4 pennen A, B, C en D zodat het circuit wordt ingeschakeld wanneer contact A wordt gesloten en een van de andere drie contacten. In dit eenvoudige geval ziet de werking van het circuit in verbale notatie er als volgt uit: “Het circuit moet stroom geleiden als contacten A en B gesloten zijn, of contacten A en C of contacten A en D. Mee eens dat het nu heel eenvoudig is om een structuurformule op te stellen. Het ziet er zo uit:
A * B + A * C + A * D = 1 of A * (B + C + D) = 1.
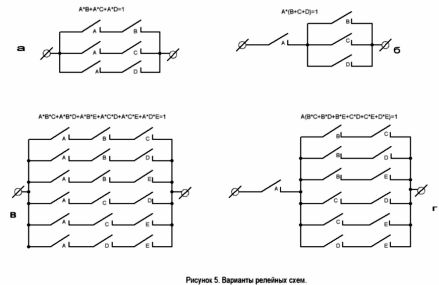
Het circuit heeft twee opties. Ze worden getoond in figuur 5. De tweede optie vereist geen relais met drie normaal open contacten.
Voorbeeld 2 Het eerste artikel was taak nummer 2 over het stemmen van sportrechters. Lees de toestand beter, het is vergelijkbaar met het zojuist onderzochte voorbeeld. Een duidelijker mondeling verslag van de vereisten ziet er als volgt uit: “Het is noodzakelijk om een circuit op te stellen met 5 contacten A, B, C, D, E, zodat het stroom geleidt en de display-lamp inschakelt als de volgende contacten gesloten zijn:
A en B en C, of A en B en D, of A en B en E, of A en C en D, of A en C en E, of A en D en E. Contact A is de voorzitterknop. Als er niet op wordt gedrukt, is elk van de 6 logische producten 0, d.w.z. Er is niet gestemd.
De structuurformule is als volgt:
(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,
of A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.
Beide varianten van het circuit zijn weergegeven in figuur 5, c en D. Dit is de oplossing voor het probleem.
Met enige vaardigheid in het lezen van structurele formules, is het gemakkelijk om het circuit van de automaat zelf en al zijn mogelijkheden voor te stellen. Interessant is dat de algebra van relaiscircuits meer informatie biedt dan zelfs het circuit zelf. Hiermee kunt u zien hoeveel en welke relais nodig zijn. Met zijn hulp kunt u eenvoudig de eenvoudigste versie van de circuitmachine vinden.
Voorbeeld 3 Nadat we enige ervaring hebben opgedaan met de voorbereiding van structurele formules, zullen we proberen het probleem dat is begonnen op te lossen eerste artikel: u moet een schakelaar ontwerpen waarmee u het licht kunt inschakelen bij het betreden van de ingang en het kunt uitschakelen nadat u naar de gewenste verdieping bent geklommen, of omgekeerd, het inschakelen bij het verlaten van het appartement en het uitschakelen nadat u naar beneden bent gegaan. Dezelfde situatie gebeurt in een lange gang: aan de ene kant moet de gloeilamp worden aangestoken en na naar de andere kant te gaan, gedoofd. Kort gezegd komt de taak neer op het bedienen van een gloeilamp vanaf verschillende plaatsen met twee schakelaars.
We kiezen de volgende procedure om het probleem op te lossen: eerst formuleren we duidelijk de bedrijfsomstandigheden van de schakelaars, vervolgens schrijven we ze in de vorm van een formule en tekenen we een elektrisch circuit op basis daarvan.
Zodat de lamp brandde (1), is het noodzakelijk dat aan een van twee voorwaarden was voldaan:
1. Schakel de schakelaar onderaan (A) in en schakel deze bovenaan uit (/ B). Ga de veranda op.
2. Schakel de schakelaar bovenaan (B) in en schakel de onderkant uit (/ A) Verlaat het appartement.
Met behulp van de geaccepteerde notatie is de structuurformule als volgt geschreven:
A * (/ B) + (/ A) * B = 1
Het schakelschema van de schakelaar is weergegeven in figuur 6. Momenteel zijn dergelijke schakelaars in de handel verkrijgbaar, dit zijn de zogenaamde doorvoer schakelaars. Daarom wordt de overweging van deze schema's hier eenvoudigweg gegeven voor het concept van de algemene principes van hun werk.
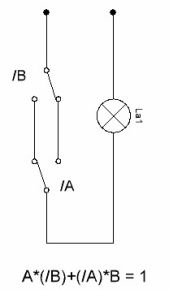
Figuur 6
In taak nr. 1 aan het begin van het eerste artikel hadden we het over een schema waarmee je het licht in de kamer kunt in- en uitschakelen met een van de drie schakelaars. Redenerend op dezelfde manier als in het geval van twee schakelaars, verkrijgen we de structuurformule:
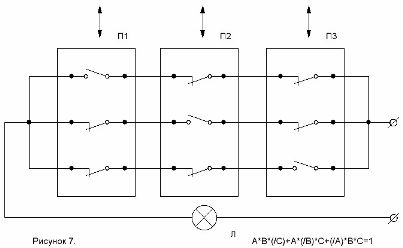
A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.
Het schema met deze formule is weergegeven in figuur 7.
Figuur 7
Aan het begin van het eerste artikel werd een eenvoudige educatieve taak nr. 2 voorgesteld: alsof er zes muren in de kamer waren en elk een schakelaar had. De logica van het circuit is exact hetzelfde als voor de drie schakelaars. Laten we ze aanduiden met de letters A, B, C, D, E, F. Bedenk dat de notatie (/ A), (/ B) enzovoort, dit geen delingsteken is, maar een logische ontkenning. Vaker aangegeven door onderstrepingstekens en, zelfs hele uitdrukkingen, bovenaan. In sommige schema's wordt dit onderstrepingsteken eenvoudig vervangen door een minteken. De structuurformule voor de zes schakelaars is dus:
(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *
(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.
Lezers worden uitgenodigd om een compleet elektrisch circuit op te stellen dat deze structurele formule implementeert om praktische vaardigheden te verwerven bij het ontwerpen van circuits. Een kleine hint: voor het circuit hebt u zes relais nodig, elk met een normaal open contact en vijf normaal gesloten. Dergelijke complexe relais, indien nodig, kunnen worden samengesteld uit meerdere eenvoudigere relais door hun spoelen parallel te verbinden.
Dit concludeert het verhaal van de Booleaanse algebra en de algebra van relaisschakelingen.
Vervolg van het artikel: Logische chips
Boris Aladyshkin
Zie ook op electro-nl.tomathouse.com
: