Booleaanse algebra. Deel 1. Een beetje geschiedenis

Op school studeerden we allemaal algebra, maar ze spraken daar niet over Booleaanse algebra. Wat is het verschil tussen Booleaanse algebra en schoolalgebra, de geschiedenis van het uiterlijk, problemen en toepassingen worden in dit artikel beschreven.

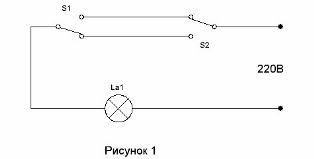
Het circuit waarmee twee schakelaars het licht in de gang bij de ingang van de gang kunnen inschakelen en uitschakelen bij het betreden van de kamer is al heel lang bekend (zie. Gang verlichtingscircuit). Het wordt getoond in figuur 1.

Taak nummer 1. Ingewikkelder. Maak een diagram waarmee u het licht in uw kamer kunt in- en uitschakelen met een van de 3 verschillende schakelaars. Schakelaars bevinden zich bij de ingang van de kamer, boven het bed en aan het bureau.

Taak nummer 2.

In een sportcommissie, zoals een fabriekscommissie, verzamelden 5 juryleden.

Elk van hen moet op verschillende beslissingen stemmen. Het besluit wordt genomen met een meerderheid van stemmen, maar alleen onder de aanvullende voorwaarde dat de voorzitter van het comité ervoor stemt.

De juryleden stemmen door op de knop te drukken die de schakelaar sluit onder de tafel waaraan ze zitten. Ze sluiten de schakelaar en stemmen voor, de cons. Teken een eenvoudig diagram waarmee u de stemresultaten automatisch kunt zien. In het eenvoudigste geval, eenvoudig met behulp van een gloeilamp - verlicht - werd de beslissing genomen, niet verlicht - nee.

Taak nummer 3. In de praktijk is dit onwaarschijnlijk, maar omdat een complexe educatieve taak heel geschikt is.

In een grote zeshoekige ruimte is op elke muur een schakelaar geïnstalleerd. Bouw een circuit zodat je op elk gewenst moment het licht in de kamer kunt in- of uitschakelen door een (willekeurige) schakelaar te draaien.

Nadat u drie tot vier dagen zonder succes over taken hebt gezeten, moet u ze tijdelijk opzij zetten. En druk worden Booleaanse algebra. Het is Booleaanse algebra, of, zoals het ook wordt genoemd, Booleaanse algebra, relaiscircuitalgebra, zal u helpen om uw problemen op te lossen.

Wat is Booleaanse algebra?

Vreemd genoeg, ondanks het feit dat ze al vijf jaar algebra op school bestuderen, zullen veel studenten, en later volwassenen, de vraag niet kunnen beantwoorden, wat is algebra? Algebra is een wetenschap die de sets van sommige elementen en de acties daarop bestudeert.

In een schoolcursus in algebra zijn dergelijke elementen getallen. Nummers kunnen niet met cijfers worden aangegeven, maar met letters, iedereen is hiermee bekend. In de eerste lessen van algebra maakt dit het voor veel studenten altijd moeilijk. Onthoud hoe moeilijk het in het begin was om te wennen aan het toevoegen van letters in plaats van cijfers, het oplossen van vergelijkingen die niets zeggen.

Waarschijnlijk stelden we onszelf vervolgens de vraag: "Waarom moeten we letters invoeren in plaats van cijfers en is dit überhaupt nodig?" En pas later zag je welke voordelen algebra biedt bij het oplossen van problemen in vergelijking met rekenen.

Algebra wordt in veel exacte wetenschappen gebruikt. Dit is natuurkunde, mechanica, sopromaat, elektriciteit. Wet van Ohm er is niets meer dan een algebraïsche vergelijking: het is voldoende om hun numerieke waarden in plaats van letters te vervangen om erachter te komen welke stroom in de belasting zal vloeien, of welke weerstand een sectie van het circuit heeft.

Zo maakte u kennis met de algebra van getallen, of met elementaire algebra. De belangrijkste en bijna unieke taak is om een ​​antwoord te krijgen op de vraag: “Wat is X gelijk aan? Hoeveel? "

Op de middelbare school bestuderen ze het begin van vectoralgebra. Deze algebra verschilt fundamenteel van elementaire algebra. Het heeft een ander karakter van de bestudeerde set en andere actieregels. Als we de vectorvergelijking oplossen, krijgen we in het antwoord een vector die geen gewoon getal is dat de vraag "Hoeveel?" Beantwoordt.

De formules van vectoralgebra verschillen in veel opzichten van de formules van elementaire algebra. In elementaire algebra en in vectoralgebra is er bijvoorbeeld een optelbewerking. Maar het wordt op totaal verschillende manieren uitgevoerd.De toevoeging van getallen is helemaal niet hetzelfde als de toevoeging van vectoren.

Er zijn andere algebra's: lineaire algebra, algebra van structuren, algebra van ringen, algebra van logica, of, wat hetzelfde is, Booleaanse algebra. Je hebt de naam waarschijnlijk niet gehoord in schoollessen. George Boole - maar iedereen kent de naam van een van zijn getalenteerde dochters Ethel Voinich (1864 - 1960). Ze schreef de roman "Gadfly", die spreekt over de strijd voor de rechten van Italiaanse carbonarians.

George Bull werd geboren in Engeland op 2 november 1815. Zijn hele leven werkte hij als leraar wiskunde en natuurkunde op school. Uit de memoires van zijn studenten is bekend welk groot belang Bul hecht aan de ontwikkeling van de creatieve vaardigheden van studenten. Met het presenteren van nieuw materiaal wilde hij ervoor zorgen dat zijn studenten zelf bepaalde formules en wetten 'herontdekken'.

De leraar vertelde studenten over de moeilijkheden waarmee wetenschappers onvermijdelijk te maken hadden bij het zoeken naar waarheid, en herhaalde graag één oosterse wijsheid: zelfs de Perzische troon kan iemand niet zoveel plezier brengen als de kleinste wetenschappelijke ontdekking. Buhl verloor nooit de hoop dat zijn studenten ooit een echte ontdekking zouden doen.

Het bereik van de wetenschappelijke interesses van Buhl was zeer breed: hij was even geïnteresseerd in wiskunde en logica - de wetenschap van wetten en vormen van denken. In die tijd werd logica als een humanitaire wetenschap beschouwd en velen die George Boole kenden, waren verbaasd over hoe de exacte cognitiemethoden die inherent zijn aan wiskunde en puur beschrijvende logica in één persoon naast elkaar konden bestaan.

Maar de wetenschapper wilde de wetenschap van wetten en denkwijzen even rigoureus maken als die van de natuurwetenschappen, zeggen wiskunde en natuurkunde. Om dit te doen, begon Boule geen getallen als letters aan te geven, zoals in gewone algebra, maar uitspraken en toonde aan dat dergelijke vergelijkingen, zeer vergelijkbaar met algebraïsche, vragen kunnen oplossen over de waarheid en valsheid van uitspraken van de mens. Dus de Booleaanse algebra ontstond.

Maar lang voordat George Buhl, de Duitse wiskundige en filosoof Gottfried Leibniz (1646-1716) voor het eerst het idee uitdrukte om een ​​wetenschap te creëren die alle concepten van gewone spreektaal met symbolen zou aanwijzen en een nieuwe algebra zou creëren voor het combineren van deze symbolen.

Na de oprichting van een dergelijke wetenschap, volgens Leibniz, zullen wetenschappers en filosofen stoppen met ruzie en schreeuwen naar elkaar, de waarheid ontdekken, maar ze zullen een potlood oppakken en rustig zeggen: "Laten we berekenen!"

Tegenwoordig is de algebra van de logica een belangrijk onderdeel van de wiskunde geworden. Een van de taken is het oplossen van allerlei vergelijkingen, waarvan de numerieke verhoudingen worden vervangen door alfabetische. Jullie hebben waarschijnlijk je hele leven lang onthouden hoe je vergelijkingen van de tweede en derde graad met lettercoëfficiënten kunt oplossen. Dus gebruikte Boole in zijn nieuwe algebra al deze formules en regels.

Wat nieuw is in de Booleaanse algebra is dat de elementen van de set die erin worden bestudeerd geen getallen zijn, maar uitspraken. Als bij het oplossen van gewone algebraïsche vergelijkingen wordt bepaald welk aantal gelijk is aan onbekende X, zoekt schoolalgebra het antwoord op de vraag: "Hoeveel?"

De algebra van de logica zoekt het antwoord op de vraag: "Is deze of die bewering aangeduid met de letter X waar?"

De betekenis en inhoud van de verklaring spelen hier geen rol. Elke bewering kan alleen waar of onwaar zijn. Het kan niet half waar en half onwaar zijn. Als voorbeeld kunnen we herinneren dat we loten gooien met een munt.

Er worden slechts twee muntstaten beschouwd - koppen of staarten. Met instemming van de partijen is de adelaar JA en zijn staarten NEE. Er worden geen andere tussenliggende punten in aanmerking genomen in de waarschijnlijkheidstheorie, hoewel ze mogelijk zijn. Een omgedraaide munt kan op een rand vallen, van de vloer naar de benen van een stoel of tafel rollen en rechtop blijven zitten, of zelfs in een brede opening in de vloer vallen. (Naar analogie met elektrische circuits kunnen de laatste twee situaties worden beschouwd als een storing in de vorm van een verbrand contact).Maar in die dagen werd de Booleaanse algebra helaas niet veel gebruikt.

Claude Shannon 'ontdekte' de Buhl-algebra opnieuw. Terwijl hij nog een student was aan het Massachusetts Institute of Technology en Amerika, bewees de jonge Claude in 1938 dat de Booleaanse algebra volledig geschikt is voor de analyse en synthese van relais- en schakelcircuits.

Met behulp van Booleaanse algebra is het heel eenvoudig om een ​​elektrisch circuit te maken van een automaat die op een relais werkt.Daarvoor blijkt dat u alleen maar precies moet weten wat de machine moet doen, dat wil zeggen dat u een algoritme nodig hebt voor de werking ervan. Dus werd de basis gelegd voor de theorie van digitale machines die werken volgens het principe van JA of NEE.

Dat is in het kort de geschiedenis van de Booleaanse algebra. In de volgende artikelen zullen we de basiswetten ervan beschouwen, voorbeelden van contactcircuits die deze wetten implementeren. Overweeg de oplossing van die taken die aan het begin van het artikel werden gegeven.

Vervolg van het artikel: Booleaanse algebra. Deel 2. Fundamentele wetten en functies

Boris Aladyshkin