categorieën: Beginnende elektriciens, Industrieel elektricien
Aantal keer bekeken: 14968
Reacties op het artikel: 4
Wat bepaalt de langdurig toegestane kabelstroom
Wat bepaalt de toelaatbare kabelstroom op de lange termijn? Om deze vraag te beantwoorden, moeten we voorbijgaande thermische processen overwegen die optreden onder omstandigheden waarin een elektrische stroom door de geleider stroomt. Het verwarmen en koelen van een geleider, zijn temperatuur, verbinding met weerstand en dwarsdoorsnede - dit alles zal het onderwerp van dit artikel zijn.
Overgangsproces
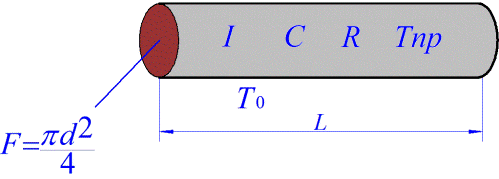
Overweeg om te beginnen een conventionele cilindrische geleider met lengte L, diameter d, dwarsdoorsnede F, weerstand R, volume V, uiteraard gelijk aan F * L, waardoor stroom I stroomt, de soortelijke warmte van het metaal waarvan de geleider is gemaakt - C, de massa van de geleider is gelijk aan
m = V * Ω,
waar Ω de dichtheid van het metaal van de geleider is, is S = pi * d * L het gebied van de zijwand waardoor koeling optreedt, Tpr is de huidige temperatuur van de geleider, T0 is de omgevingstemperatuur en dienovereenkomstig is T = Tpr - TO de temperatuurverandering. KTP is de warmteoverdrachtscoëfficiënt, die numeriek de hoeveelheid warmte aangeeft die wordt overgedragen van een oppervlakte-eenheid van een geleider in 1 seconde bij een temperatuurverschil van 1 graad.
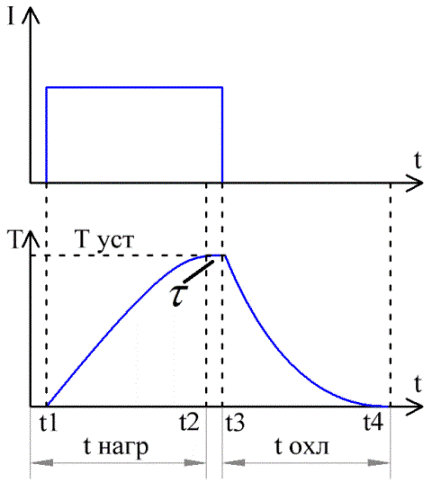
De afbeelding toont de grafieken van de stroom en temperatuur in de geleider in de tijd. Van tijd t1 tot tijd t3 vloeide stroom I door de geleider.
Hier kunt u zien hoe, na het inschakelen van de stroom, de temperatuur van de geleider geleidelijk stijgt en op het tijdstip t2 ophoudt te stijgen, stabiliseert. Maar na het uitschakelen van de stroom op tijdstip t3 begint de temperatuur geleidelijk te dalen en op tijdstip t4 wordt deze weer gelijk aan de beginwaarde (TO).
Het is dus mogelijk om de vergelijking van de warmtebalans op te schrijven, een differentiaalvergelijking voor het verwarmingsproces van de geleider, waarbij wordt weerspiegeld dat de warmte die op de geleider vrijkomt gedeeltelijk wordt geabsorbeerd door de geleider zelf, en gedeeltelijk wordt gegeven aan de omgeving. Hier is de vergelijking:
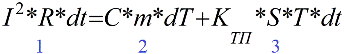
Aan de linkerkant van vergelijking (1) staat de hoeveelheid warmte die vrijkomt in de geleider gedurende de tijd dt, de doorgang van stroom I.
De eerste term aan de rechterkant van vergelijking (2) is de hoeveelheid warmte die wordt geabsorbeerd door het geleidermateriaal, van waaruit de temperatuur van de geleider met dT graden steeg.
De tweede term aan de rechterkant van vergelijking (3) is de hoeveelheid warmte die gedurende de tijd dt van de geleider naar de omgeving is overgedragen en is gerelateerd aan het oppervlak van de geleider S en het temperatuurverschil T door de warmtegeleidingscoëfficiënt Ktp.
Ten eerste, wanneer de stroom wordt ingeschakeld, wordt alle in de geleider afgegeven warmte gebruikt om de geleider direct te verwarmen, wat leidt tot een verhoging van de temperatuur, en dit komt door de warmtecapaciteit C van het geleidermateriaal.
Bij toenemende temperatuur neemt het temperatuurverschil T tussen de geleider zelf en de omgeving dienovereenkomstig toe, en de gegenereerde warmte gaat al gedeeltelijk de omgevingstemperatuur verhogen.
Wanneer de temperatuur van de geleider een stabiele stabiele waarde van Tust bereikt, wordt op dit moment alle warmte die vrijkomt van het oppervlak van de geleider overgedragen naar de omgeving, zodat de temperatuur van de geleider niet langer stijgt.
De oplossing voor de differentiaal warmtebalansvergelijking is:
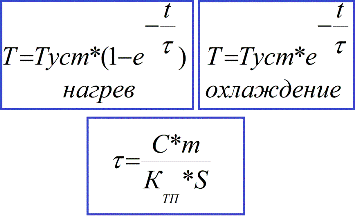
In de praktijk duurt dit tijdelijke proces niet meer dan drie tijdconstanten (3 * τ), en na deze tijd bereikt de temperatuur 0,95 * Tust. Wanneer het overgangsproces van verwarmen stopt, wordt de vergelijking van de warmtebalans vereenvoudigd en kan de steady-state temperatuur gemakkelijk worden uitgedrukt:
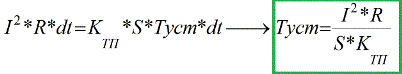
Toelaatbare stroom
Nu kunnen we komen tot wat de stroom precies waardeert als een toelaatbare stroom op lange termijn voor een geleider of kabel. Vanzelfsprekend is er voor elke geleider of kabel een bepaalde normale continue temperatuur, volgens de documentatie.Dit is zo'n temperatuur waarbij een kabel of draad continu en voor een lange tijd zonder schade aan zichzelf en aan anderen kan zijn.
Uit de bovenstaande vergelijking wordt duidelijk dat een specifieke stroomwaarde geassocieerd is met een dergelijke temperatuur. Deze stroom wordt genoemd toelaatbare kabelstroom. Dit is zo'n stroom, die, wanneer hij lange tijd door de geleider gaat (meer dan drie tijdconstanten), deze verwarmt tot een toelaatbare, dat wil zeggen normale temperatuur Tdd.
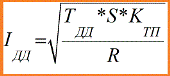
Hier: Idd - toelaatbare stroom op lange termijn; TDD - toelaatbare geleidertemperatuur.
Om praktische problemen op te lossen, is het het handigst om de toelaatbare stroom op lange termijn te bepalen volgens speciale tabellen van de PUE.
In het geval van een kortsluiting stroomt een aanzienlijke kortsluitstroom door de geleider, die de geleider aanzienlijk kan verwarmen en de normale temperatuur overschrijdt. Om deze reden worden geleiders gekenmerkt door een minimale doorsnede op basis van de toestand van kortstondige verwarming van de geleider door een kortsluitstroom:
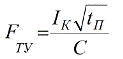
Hier: Ik - kortsluitstroom in ampères; tp is de kortere kortsluitstroomduur in seconden; C is een coëfficiënt die afhankelijk is van het materiaal en de constructie van de geleider en van de toelaatbare temperatuur op korte termijn.

Sectie Verbinding
Laten we nu kijken hoe de toelaatbare stroom op lange termijn afhangt van de doorsnede van de geleider. Na het oppervlak van de zijwand door de diameter van de geleider tot uitdrukking te hebben gebracht (de formule aan het begin van het artikel), ervan uitgaande dat de weerstand gerelateerd is aan het dwarsdoorsnedeoppervlak en de specifieke weerstand van het materiaal van de geleider, en de bekende formule voor weerstand te vervangen door de hierboven gegeven formule voor Idd, verkrijgen we voor een langdurige toegestane huidige Idd-formule :
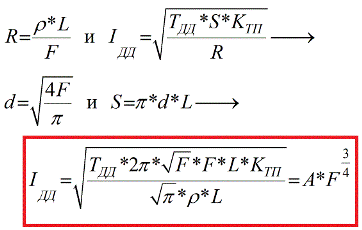
Het is gemakkelijk om te zien dat de verbinding tussen de op de lange termijn toelaatbare stroom van de geleider Idd en de doorsnede F niet direct evenredig is, hier wordt het dwarsdoorsnedegebied verhoogd tot het vermogen ¾, wat betekent dat de toelaatbare stroom op de lange termijn langzamer toeneemt dan de dwarsdoorsnede van de geleider. Andere constanten, zoals soortelijke weerstand, warmteoverdrachtscoëfficiënt, toelaatbare temperatuur, zijn per definitie individueel voor elke geleider.
In feite is het zo dat de afhankelijkheid niet direct kan zijn, want hoe groter de dwarsdoorsnede van de geleider, hoe slechter de koelomstandigheden van de binnenste lagen van de geleider, hoe meer acceptabele temperatuur wordt bereikt bij een lagere stroomdichtheid.
Als u geleiders met een grotere doorsnede gebruikt om oververhitting te voorkomen, leidt dit tot een overmatig materiaalverbruik. Het is veel voordeliger om meerdere geleiders met een kleine dwarsdoorsnede parallel te gebruiken, dat wil zeggen multicore geleiders of kabels te gebruiken. En de relatie tussen de toelaatbare stroom op lange termijn en het dwarsdoorsnedegebied als geheel blijkt als volgt:
Stroom en temperatuur
Om de temperatuur van een geleider met een bekende stroom en gespecificeerde externe omstandigheden te berekenen, moet u rekening houden met de stabiele toestand wanneer de temperatuur van de geleider Tust bereikt en niet langer toeneemt. Initiële gegevens - stroom I, warmteoverdrachtscoëfficiënt Ktp, weerstand R, zijwandgebied S, omgevingstemperatuur T0:
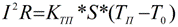
Een vergelijkbare berekening voor continue stroom:
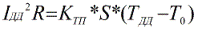
Hier wordt TO genomen als de berekende omgevingstemperatuur, bijvoorbeeld + 15 ° C voor onder water en in de grond, of + 25 ° C voor buiten. De resultaten van dergelijke berekeningen worden gegeven in tabellen van continue stromingen, en voor lucht nemen ze een temperatuur van + 25 ° C, omdat dit de gemiddelde temperatuur van de warmste maand is.
Door de eerste vergelijking door de tweede te delen en de temperatuur van de geleider uit te drukken, kunnen we een formule verkrijgen voor het vinden van de temperatuur van de geleider bij een andere stroom dan de toegestane lange termijn, en bij een gegeven omgevingstemperatuur, als een lange termijn toelaatbare stroom en een toegestane temperatuur op lange termijn bekend zijn, en u niet hoeft te toevlucht te nemen tot het gebruik van andere constanten:
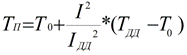
Uit deze formule blijkt dat de temperatuurstijging evenredig is met het kwadraat van de stroom, en als de stroom met 2 keer toeneemt, zal de temperatuurstijging met 4 keer toenemen.

Als externe omstandigheden afwijken van het ontwerp
Afhankelijk van de werkelijke externe omstandigheden, die kunnen verschillen van de berekende, afhankelijk van de manier van leggen, bijvoorbeeld meerdere geleiders (kabel) die parallel zijn geplaatst of in de grond liggen bij een andere temperatuur, is een aanpassing van de maximaal toelaatbare stroom vereist.
Vervolgens wordt de correctiefactor Kt geïntroduceerd, waarmee de toelaatbare stroom op lange termijn wordt vermenigvuldigd onder bekende (tabel) omstandigheden. Als de buitentemperatuur lager is dan de berekende, dan is de coëfficiënt groter dan één; als deze hoger is dan de berekende, dan is Kt dienovereenkomstig minder dan één.
Wanneer meerdere parallelle geleiders zeer dicht bij elkaar worden gelegd, zullen ze elkaar bovendien verwarmen, maar alleen als de omgeving stilstaat. Feitelijke omstandigheden leiden er vaak toe dat de omgeving mobiel is (lucht, water) en convectie leidt tot koeling van de geleiders.
Als het medium bijna stationair is, bijvoorbeeld bij het leggen in een buis onder de grond of in een kanaal, zal wederzijdse verwarming een afname van de toelaatbare stroom op lange termijn veroorzaken en hier moet u de correctiefactor Kn opnieuw invoeren, die wordt gegeven in de documentatie voor kabels en draden.
Zie ook op electro-nl.tomathouse.com
:
